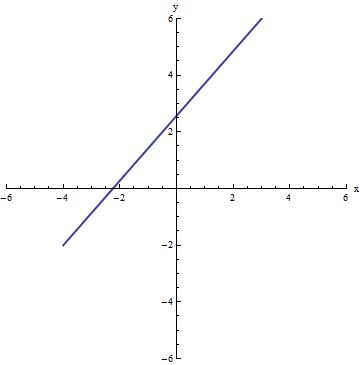 |
 |
Below are two representations of the parametric curve
x=3t+(1-t)(-4)
y=6t+(1-t)(-2)
with t between 0 and 1.
If you eliminate the parameter t, you see this is a linear line segment between the points (-4,-2) and (3,6).
 |
 |
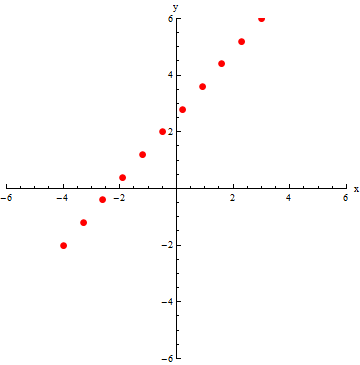
The second representation is the table of (x,y) pairs found from choosing values of t between 0 and 1 with constant step size of 0.1.
| t | x | y |
|---|---|---|
| 0 | -4 | -2 |
| 0.1 | -3.3 | -1.2 |
| 0.2 | -2.6 | -0.4 |
| 0.3 | -1.9 | 0.4 |
| 0.4 | -1.2 | 1.2 |
| 0.5 | -0.5 | 2 |
| 0.6 | 0.2 | 2.8 |
| 0.7 | 0.9 | 3.6 |
| 0.8 | 1.6 | 4.4 |
| 0.9 | 2.3 | 5.2 |
| 1.0 | 3 | 6 |
This table of values shows us that if the parametric representation is being used to describe a particle's motion, the particle would begin at (-4,-2) and move to (3,6). The is something a y=f(x) description of the line segment would be unable to convey.
We can use an animation to illustrate the motion of the particle. Below, the line segment between (-4,-2) and (3,6) is represented by two different parameterizations (blue line). An animation of a particle moving across the curve (red dot) that is obtained by evaluating the parameterizations at the same t values (t goes from 0 to 1 by 0.02). Since the time step is constant, this gives a good visual representation of the velocity of the particle.
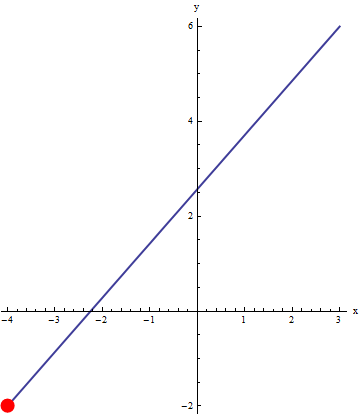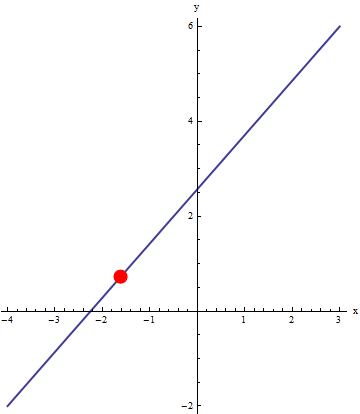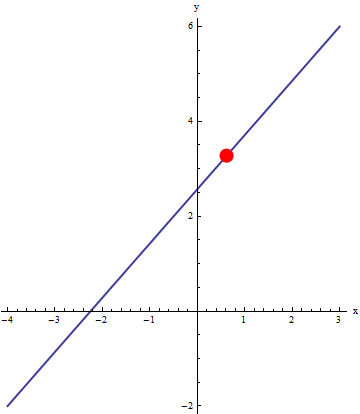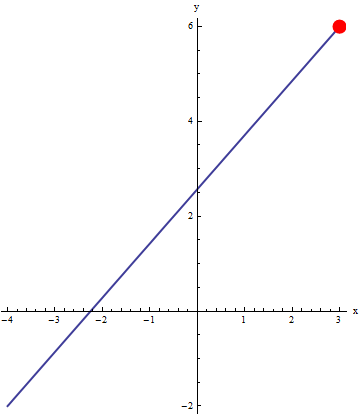 |
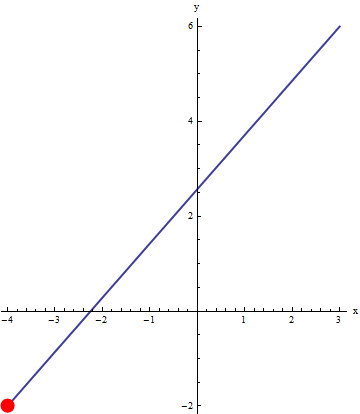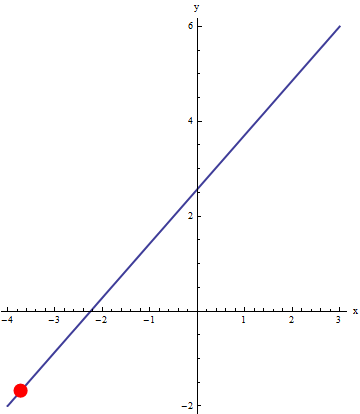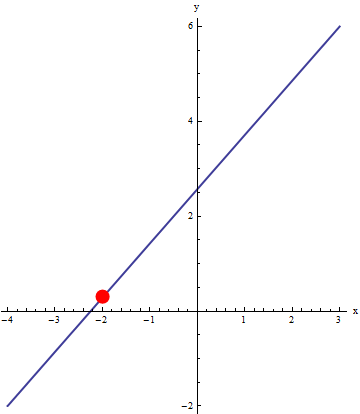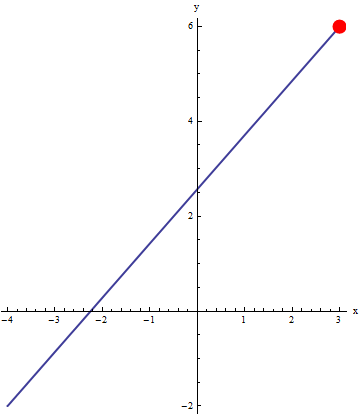 |
|
x=3t+(1-t)(-4) y=6t+(1-t)(-2) with t between 0 and 1. |
x=3t3+(1-t3)(-4) y=6t3+(1-t3)(-2) with t between 0 and 1. |
Notice the particle on the left moves with constant velocity, but the particle on the right has varying velocity (slower at the start). This ability to imbed velocity into a parametric representation makes it a useful representation indeed! Since one interpretation of a derivative (instantaneous rate of change) is velocity, the velocity of parametric representations is something you will see in calculus.
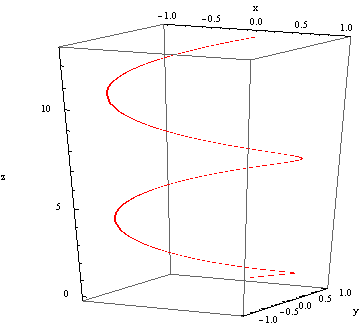
Parametric representations extend easily to higher dimensions. For example, we can represent a helix by
x=cos(t)
y=sin(t)
z=t
 |
One useful feature of parametric representations can be seen when thinking about a circle
x2 + y2 = r2. This
implicit representation contains both the top and bottom of the circle, which we cannot do if we tried to use an explicit function
(you would need to consider y = f1(x) = sqrt(r2-x2) and
y = f2(x) = - sqrt(r2-x2)
separately). Parametric representations can also describe the entire circle at once, like the implicit representation could,
and can of course imbed a velocity component as well (which the implicit could not) if the circle represents the motion of a particle.
The following all describe the set of points (x,y) such that x2 + y2 = r2 (the
first being the most common):
x = r cos(t)
y = r sin(t)
t between 0 and 2 pi
x = r cos(2t)
y = r sin(2t)
t between 0 and pi
x = r cos(t2)
y = r sin(t2)
t between 0 and sqrt(2 pi)
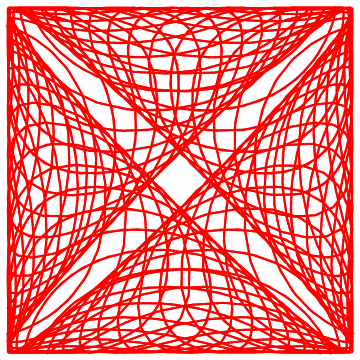
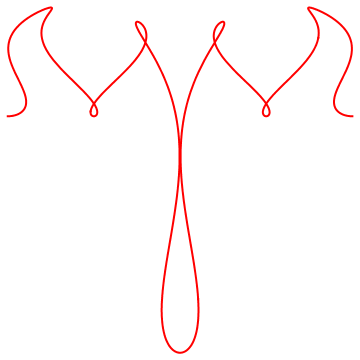
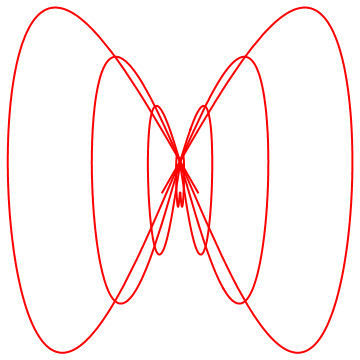
Parametric representations can be used to represent complicated curves. Imagine trying to sort out a y=f(x) representation of what is below! Every failure of the vertical line test would result in another explicit function y=f(x). These cool curves all involve a trig function to introduce some periodicity into the curve.
 |
 |
 |
 |
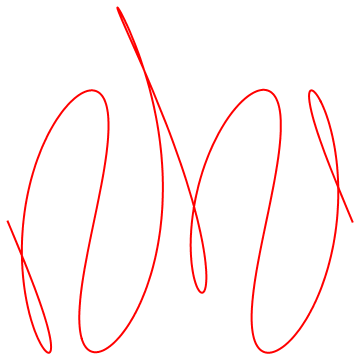 |
 |
 |