Complete Graphs

[Graphics:HTMLFiles/counting_1.gif]

[Graphics:HTMLFiles/counting_2.gif]

[Graphics:HTMLFiles/counting_3.gif]

[Graphics:HTMLFiles/counting_4.gif]

[Graphics:HTMLFiles/counting_5.gif]

[Graphics:HTMLFiles/counting_6.gif]

Counting

Using a Computer to Calculate Hamiltonian Circuits

The number of Hamiltonian circuits on a complete graph with 25 vertices:

In[11]:=

(25 - 1) !/2

Out[11]=

310224200866619719680000

The number of seconds in a year:

In[12]:=

60second/minute×60minute/hour×24hour/day×365day/year

Out[12]=

(31536000 second)/year

The number of years it would take to find all the Hamiltonian circuits in the graph:

In[13]:=

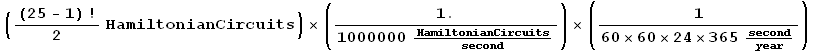
((25 - 1) !/2HamiltonianCircuits) × (1./(1000000HamiltonianCircuits/second)) × (1/(60×60×24×365second/year))

Out[13]=

9.83714*10^9 year

which is almost ten billion years!

Using a Much Faster Computer to Calculate Hamiltonian Circuits

Let's say we have access to the 99th fastest computer on the planet. http://www.iastate.edu/~nscentral/news/06/sep/lightning.shtml

This computer can perform 1.8 trillion calculations per second. Let's say that a "calculation" is computing the length of a Hamiltonian circuit (which in reality is far more than a single calculation). How long would it take now?

In[14]:=

((25 - 1) !/2HamiltonianCircuits) × (1./(1.8×10^12HamiltonianCircuits/second)) × (1/(60×60×24×365second/year))

Out[14]=

5465.08 year

It still takes 5000 years to implement the brute force algorithm for a complete graph on 25 vertices! But that's a significant improvement over ten billion years, so maybe computers are the way to go after all. But we see they aren't since for a complete graph on 29 vertices we are up to 2 billion years again.

In[15]:=

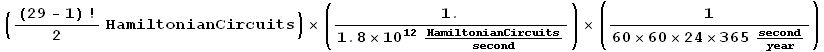
((29 - 1) !/2HamiltonianCircuits) × (1./(1.8×10^12HamiltonianCircuits/second)) × (1/(60×60×24×365second/year))

Out[15]=

2.68554*10^9 year

Created by Mathematica  (January 24, 2007) Valid XHTML 1.1!